「相対論 超概論」

2011年10月01日作成　 　1page　　2page　　3page　

相対論的エネルギーと E=mc²

相対性理論の有名な公式に、エネルギーと質量の変換性を示すE = mc²という式があります。この式について少し解説しましょう。今までの議論は数学の知識をほとんど必要としませんでしたが、この節だけは多少の数学の知識 （高校生程度） を前提として説明します。

ニュートン力学の世界では空間と時間は完全に別個のパラメーターでしたが、相対論ではローレンツ変換によって時間と空間が相互に依存して変換されます。そのため、空間と時間を別個に扱うのではなく、一まとめにして扱うと便利です。それで、物体の座標を、時間1次元と空間3次元からなる4元ベクトルで表わすことにします。成分表示すると、

です。さて、よく知られているように、速度とは位置座標を時間で微分して定義されます。x、y、z方向の速度をそれぞれv_x、v_y、v_zとすると、

です。しかし相対論では、運動する物体によって時間が相対的ですので、どのように時間で微分するかが問題になります。一番適切なのは、物体と共に運動する時計の刻む時間で微分することでしょう。これは、前節で導入した、運動する座標系の原点にある時計の時間に他なりません。これを"固有時"といい、τで表わします。つまり、

となります。この固有時で先ほどの座標を微分すると、

となることに注意して、次の4元速度が得られます。

さらに、ニュートン力学では速度に質量mを掛けて運動量pを定義します。これに倣い、"4元運動量"を次のように定義しましょう。

ここで、4元運動量の空間成分p_x、p_y、p_zはニュートン力学の運動量の相対論的拡張とみなすことができますが、時間成分p_tの意味するところは何でしょうか？実は、これが"相対論的エネルギー"に相当します。つまり、相対論では、時間と空間だけでなく、エネルギーと運動量も統一的に扱われるのです。次元を合わせるためにエネルギーEをcで割り、E/c = p_tとして、

がエネルギーの表式になります。γがvの関数なのでこのEはvに依存しますが、ここでv = 0とするとE = mc2が得られ、物体は最低でも速度によらない"質量エネルギー"mc²を持つことになるのです。

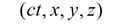
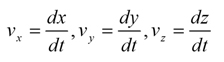
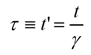
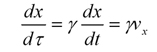
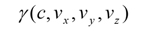
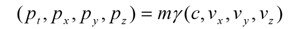
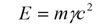
E = mc²は、質量からエネルギーへの変換、またエネルギーから質量への変換が可能であることを意味しています。この式の応用を１つだけご紹介することにします。

太陽では、水素原子4個をヘリウム原子１個に変換する核融合反応が絶えず起こっています。このとき、生成されたヘリウム原子の質量は反応前の水素原子4個の質量よりわずかに軽くなります。失われた質量はE = mc²にしたがってエネルギーに変換され、そのエネルギーの一部が地球の私達の元に届いているのです。では、太陽で毎秒どれほどの質量がエネルギーに変換されているのかを計算してみましょう。

地球上で1秒当たりの太陽エネルギーを測定すると、1340 W/m² となります（Wの次元はm²･kg/s³ です）。また、地球と太陽の間の距離は、平均して1.50×10¹¹ mです。この距離を半径とする巨大な球面を考えると、その表面積は4π（1.50×10¹¹）² m² になり、これに1340 W/m² をかけると太陽が1秒間に放出するエネルギーが求められます。このエネルギーに相当する質量は、E = mc²の式から、エネルギーをc²で割れば算出することができます。cを3.0×108 m/s2、円周率πを3.14として計算すると、

となりますから、約400万トンの質量が1秒間にエネルギーに変わっていることになります。これは、太陽が毎秒400万トンずつ軽くなっていることを意味しますが、それでも太陽が消えてなくなったりしないのは、元々太陽が非常に巨大であるからに他なりません。太陽の質量を2.0×10³⁰ kg、1年の秒数を3.15×10⁷ sとして、1年間にエネルギーとなって失われる太陽質量の割合を計算してみてください。

一般相対性理論

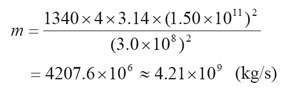
特殊相対論はニュートン力学に多くの修正を要求しましたが、それだけでは重力理論としてのニュートン力学に取って代わるものではありません。相対性理論がニュートン力学を完全に凌駕するには、重力の効果を理論に取り入れた一般相対性理論の完成を待たなければなりませんでした。最後に一般相対性理論についてごく簡単に触れることにします。

特殊相対性理論の「特殊」とは、座標系として慣性系のみを考慮するという意味でした。すると、一般相対性理論とは、座標系を限定せず、0でない任意の加速度を持つ座標系（"加速度系"）について議論を一般化した相対性理論であろうということが容易に推察でき、事実その通りです。

つまり、特殊相対性原理は次のように一般化されます。

● 慣性系に限らず、すべての座標系で、物理法則は同じ形を取る。

これを"一般相対性原理"といいます。すなわち、ローレンツ変換だけでなく、任意の座標変換で物理法則が不変であることを要請する原理です。しかし、この原理だけではまだ重力については何も言っていません。アインシュタインは、加速度系と重力場を結びつける次の原理を提唱しました。

● 重力場における重力は適当な加速度系での慣性力を用いて相殺することができる。

これは"等価原理"と呼ばれます。慣性力とは、電車やエレベーターなどが動き出したときに進行方向と逆に感じる力のことです。この原理により、重力がある座標系においても、適当な加速度系に座標変換することで重力をどんな値にも（ゼロにも）することができます。また逆に、外力の働いていない慣性系からの座標変換によって、重力を生じさせることもできます。こうして、慣性系における特殊相対性理論を、重力場のある座標系へ拡張し、さらに一般相対性原理の要請から物理法則の形を決定する道が開かれました。

この2つの原理を出発点として、アインシュタインは重力場の新しい方程式を提唱しました。アインシュタイン方程式と呼ばれるこの方程式を解くことにより、ブラックホールや膨張宇宙といった画期的な概念が提唱され、私達の宇宙に対する理解は大幅に深まりました。一方、重力が主役のマクロな世界を説明する一般相対性理論と、量子論に支配されるミクロな世界を統一する量子重力理論は、未だに完成していません。相対論の登場から100年を経た現代物理学の潮流は、自然界の4つの力を統一する究極の理論の完成を目指しています。

参考文献

本稿の執筆に当たり、下記の文献を参考にしました。

● 相対性理論 内山龍雄 岩波文庫 物理テキストシリーズ8（1977）

● 相対性理論 アインシュタイン 内山龍雄訳・解説 岩波文庫（1988）

● 相対性理論入門講義 風間洋一 培風館 現代物理学入門講義シリーズI（1997）